What would happen if you keep a block of wood between the two plates of a capacitor? How would the capacitance associated with the system adjust to this ‘intrusion’? Read on to find out how the capacitance involving combinations of such ‘dielectrics’ is evaluated.

Based on the changes in the quantities observed, we classify that wood behaves as a dielectric of a certain dielectric constant 'k'. Even water or air or wool could replace wood in our example, each exhibiting a different ‘k’.
Now look at an example with three different dielectrics placed between the capacitor plates as shown. Let their dielectric constants be k1,k2 and k3. Throughout the analysis consider the area of the capacitor plate shown below to be ‘A’ and the width of each capacitor,‘d’.
Our objective is to find the equivalent capacitance. Thinking in the language of circuits, what might be strikingly evident in this configuration is that the part with dielectric k1 can be assumed to be in ‘series’ with the ‘parallel’ combination of dielectrics k2 and k3.
Using the formula for capacitance as:
we get,

and

The factor of half is contributed by the truncated area. The resultant of C2 and C3 in parallel, say C4 , is :
Now, this resultant is in series with the capacitor of capacitance C1 of dielectric k1.
Therefore the resultant capacitance, C, is :
which gives us,
There exists another way of looking at this.
Divide the dielectric k1, along the line dividing k2 and k3. Now we visualize the system as a combination of four different capacitors. The way in which they are connected can be analyzed from the figure below.
Therefore the resultant capacitance can be found out by considering the series combination of k1 and k2 to be in parallel with the series combination of k1 and k3.
The capacitance C5 of the series combination of first and second capacitors is,
where
Similarly C6 can be determined. Therefore, the net capacitance is,
After solving this problem in two different ways, we’ve realized that all roads have actually not led to Rome. Which one led us to the destination safely?
The second one. Let us see why.
In the first pathway we have considered that k2 and k3 are parallel. This is the flaw as the potential difference between the boundary dividing k1 and k2-k3 need not be constant, i.e., it is not given to be an equipotential surface. By making them parallel we have violated this rule!
Note: As a special case if k2 = k3, both methods will yield correct answer. Convince yourself and find out why this anomaly rises! (Hint: Now, what happens to the potential throughout the boundary?)









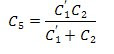


0 comments:
Post a Comment