Two countries A and B are at war with each other. Since both of them are equally matched in air and on land, they decide to fight at sea. You are a citizen defending country A which has better naval fleet than B. On the verge of defeat, as a last resort, country B sends one of their best submarines to attack from below. How do you employ the physics of sound as a weapon at this decisive moment, to save your nation? Read on to discover...

Unfortunately, the captain in that submarine, a very shrewd man, has outsmarted every other submarine of yours and is already inside the enemy territory. The launch sequence attacking your country has been started and you have little time left before your fleet is bombarded and your fate sealed.
The only way out would be to locate and destroy the submarine by determining its speed and trajectory and then launching a missile at it. The SONAR system in your submarine emits waves of frequency 198 kHz. However the detector indicates that sound waves of constant frequency 202 Hz are received. Can we, somehow answer the above problem with this minimal data obtained?
At first sight, it seems rather curious that the reflected waves received are of higher frequency. This common-but-bizarre phenomenon is what is known as the Doppler Effect. It illustrates the change in frequency of sound heard by the observer when the object and source are moving relative to each other.
Why does this happen?
Suppose that you are a stationary observer in the ocean and a stationary submarine emits a sound of constant frequency as shown

Every successive wave reaches you after equal intervals of time, due to which the observed frequency is same as the emitted frequency.
Suppose that, now, the submarine starts moving towards you. Each wave is emitted at a distance slightly closer to you than the previous one. In other words, newer waves have less distance to cover before they reach you. As a result, every wave that follows takes less time to reach you than its predecessor.

Describing this figuratively, the waves reach you in a 'bunch' and you hear a sound of higher frequency.
Let’s assume that the object and source, both move along a straight line in the same direction. If the source emits a sound of frequency ‘ν’, the frequency perceived by the observer is given by an essential relation which is,
When the directions of either of the velocities change, the sign also changes.
Coming back to our scenario, since the observed frequency is greater than the expected, we conclude that the submarine is travelling directly towards you. Next, we need to find the speed of the submarine. Now, how is that done using this relation?
Firstly, analyze the wave that reached you. This wave which was initially sent by you to the submarine has reflected off it and reached you. Hence, assign a frequency of νˡˡ to it. Remember, you’re stationary during the whole process. If νˡ was what received by the target submarine, then,
where, vsound =1500m/s , vsub = speed of the submarine and νˡˡ=202Hz.
Now, the problem reduces to finding what νˡ is.
Absorbing this into our first relation brings us to -

Substituting the numerical values gives us that the submarine is approaching us at the rate of 15 meters per second. The captain is now alerted that some device has detected him and veers off the direction without altering his speed. This translates to a change in the frequency observed. Your reading shows 200Hz suddenly and starts decreasing gradually. Is there a way to determine the angle, say θ, made by his new path with the old one?
In such a case, where an oblique path is followed to pass by the observer, the components of the velocities along the line joining the two entities, only, come to play. This is the more general case of the effect. The frequency of the sound of the siren of an ambulance that passes by, gradually, reaches a maximum when it’s closest and proceeds to decrease. This is because it only passes by and not runs into us.

Going by this statement, the frequency relation abruptly changes to the following at the instant he changes direction.

This equation leaves the value of the cosine of that angle at a value close to half. Hence it is a good approximation rounding it to 60o. Assuming you have less than a minute to act, you fire a torpedo at a speed of 8ms-1 at the instant you detect this change of path. What follows is the termination of the frequency received from the submarine once it drops down to 198Hz. If the target was 340m away from you when the torpedo was launched, what should have been the direction of launch and the time taken for impact?

The observed frequency matches with the real frequency when the line joining the source and the observer is exactly perpendicular to the path of the source. You realize this when you try the generalized equation for an angle of 90 o .
What’s more needed is merely the knowledge of Pythagoras’ theorem! If ‘t’ is the time that the torpedo took to hit the submarine, then, the submarine is ‘15t’ meters away from its graveyard, and the torpedo ‘8t’ meters away from its destination. These values are arrived at, by the relation between speed, time and distance.
This gives,
Hence the missile is fired at a 30 o angle and strikes the submarine after 20s. Now that we’ve answered every part of our problem, Cry havoc and let slip the dogs of war!!!

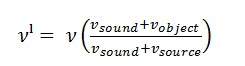




0 comments:
Post a Comment